녕의 학습 기록
백준_11437 LCA (최소공통조상 일반) 본문
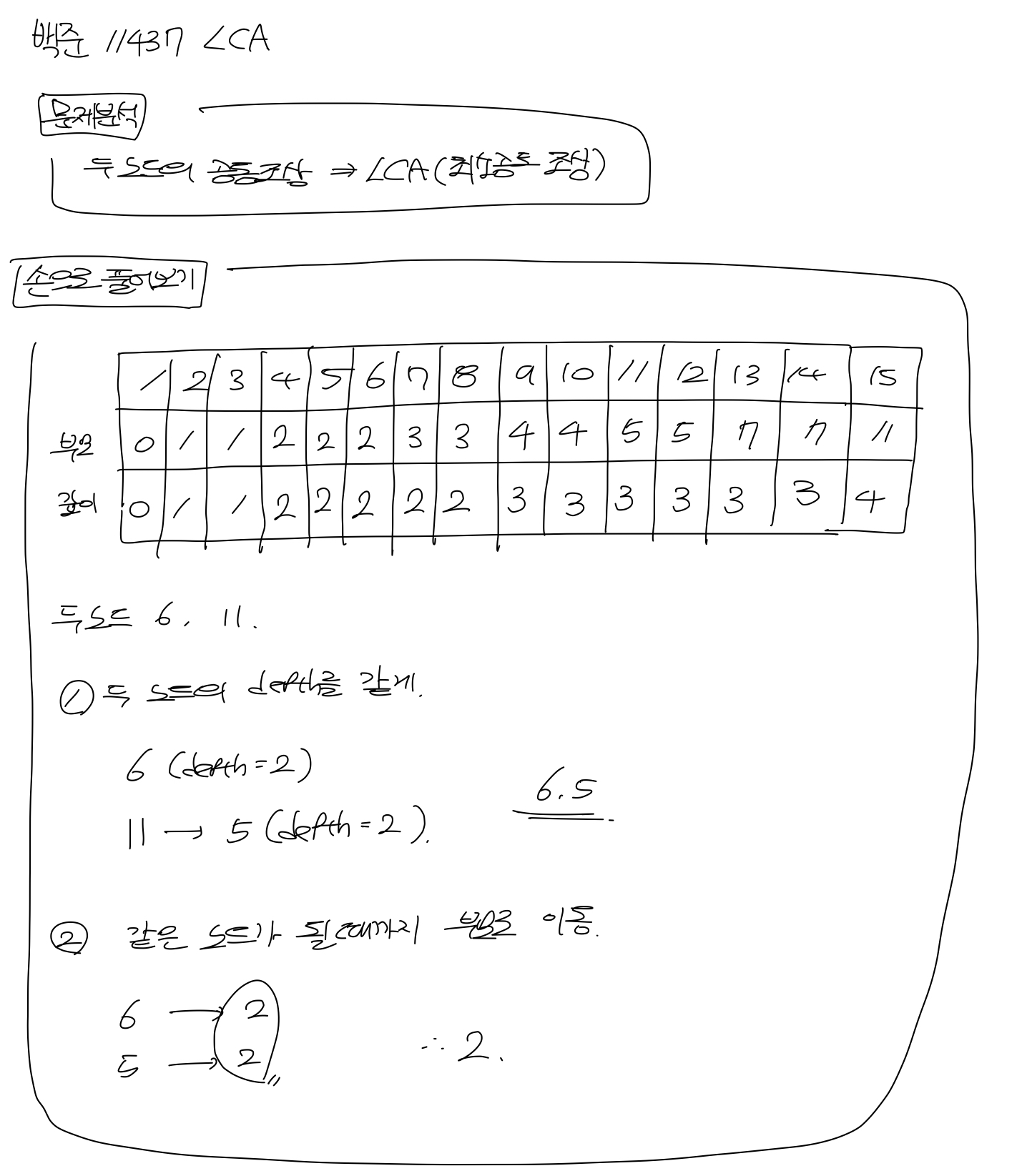
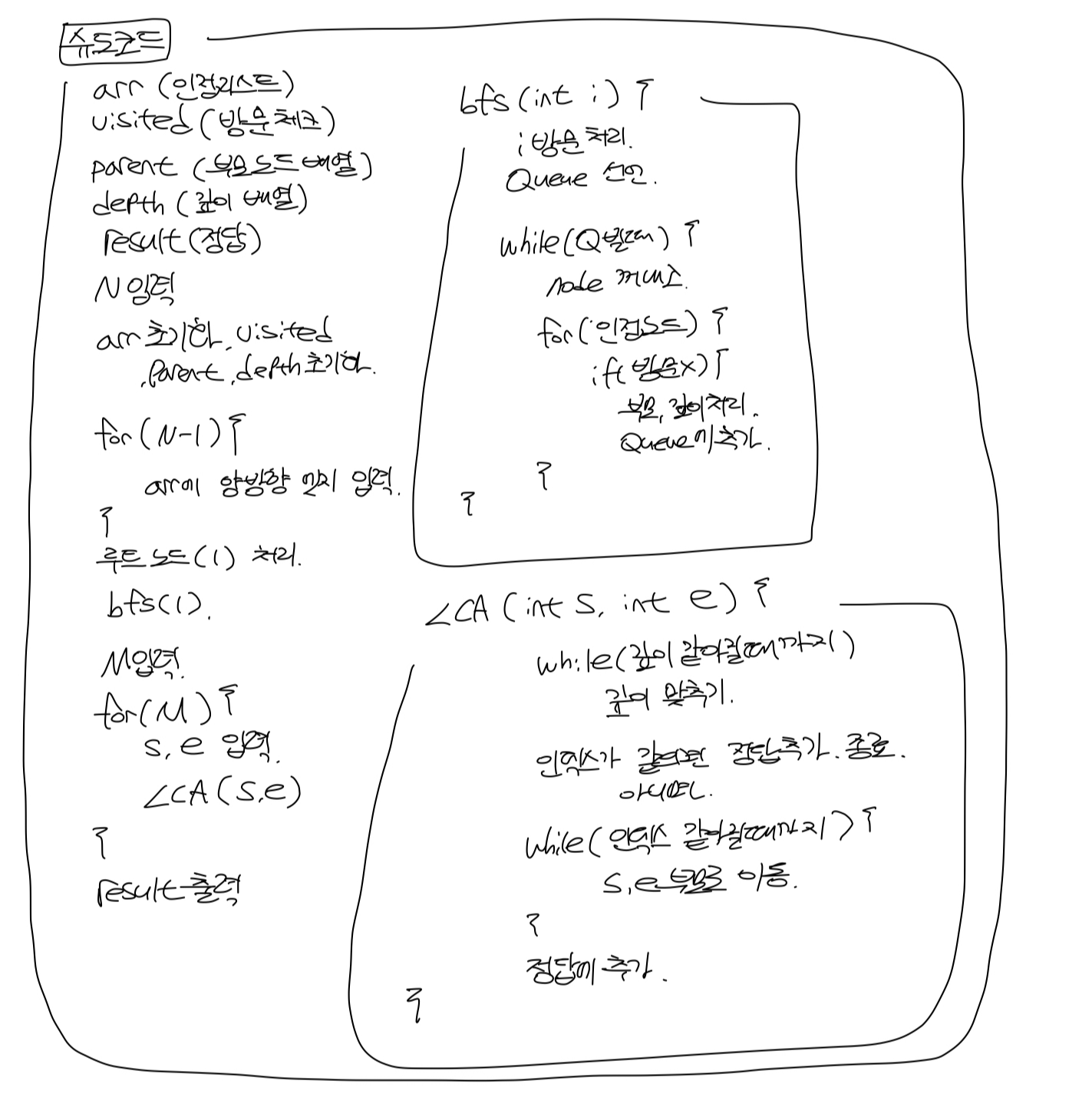
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class BJ_11437_LCA {
static ArrayList<Integer>[] tree;
static boolean[] visited;
static int[] parent;
static int[] depth;
static StringBuilder result = new StringBuilder();
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
tree = new ArrayList[n + 1];
visited = new boolean[n + 1];
parent = new int[n + 1];
depth = new int[n + 1];
int i;
for (i=1; i<n+1; i++) {
tree[i] = new ArrayList<>();
}
StringTokenizer st;
int a, b;
for (i=0; i<n-1; i++) {
st = new StringTokenizer(br.readLine(), " ");
a = Integer.parseInt(st.nextToken());
b = Integer.parseInt(st.nextToken());
tree[a].add(b);
tree[b].add(a);
}
//루트 노드 처리
parent[1] = 0;
depth[1] = 0;
bfs(1);
int m = Integer.parseInt(br.readLine());
for (i=0; i<m; i++) {
st = new StringTokenizer(br.readLine(), " ");
a = Integer.parseInt(st.nextToken());
b = Integer.parseInt(st.nextToken());
lca(a, b);
}
System.out.println(result);
}
static void bfs(int root) {
Queue<Integer> queue = new LinkedList<>();
visited[root] = true;
queue.add(root);
int nowNode;
while (!queue.isEmpty()) {
nowNode = queue.poll();
for (int nextNode : tree[nowNode]) {
if (visited[nextNode] == false) {
parent[nextNode] = nowNode;
depth[nextNode] = depth[nowNode] + 1;
visited[nextNode] = true;
queue.add(nextNode);
}
}
}
}
static void lca(int a, int b) {
if (depth[a] < depth[b]) { //무조건 a가 더 깊게끔 설정
int temp = b;
b = a;
a = temp;
}
while (depth[a] != depth[b]) {
a = parent[a];
}
while (a != b) {
a = parent[a];
b = parent[b];
}
result.append(a).append('\n');
}
}11437번: LCA
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net
'Algorithm > Algorithm 문제' 카테고리의 다른 글
| 백준_11050 이항 계수 1 (조합) (0) | 2024.03.24 |
|---|---|
| 백준_11438 LCA2 (빠른 최소 공통 조상) (0) | 2024.03.19 |
| 백준_11505 구간 곱 구하기 (세그먼트 트리) (1) | 2024.03.17 |
| 백준_10868 최솟값 (세그먼트 트리) (0) | 2024.03.16 |
| 백준_2042 구간 합 구하기 (세그먼트 트리) (0) | 2024.03.16 |




